A short introduction to the pi-calculus
Overview
This is a short introduction to the pi-calculus for readers unfamiliar with process algebra. It informally introduces the basic concepts of the pi-calculus and allows for getting a grasp of the formulas.
Agents and Names
The pi-calculus is based on the concepts of names and agents. A name is a collective term for things like links, pointers, references, identifiers and so on. These names could be used to synchronize actions between a community of concurrent agents. Each agent represents a process; a description of a timely and logical sequence of things to do. When one agent wants to talk to another agent they use a common name for communication (for the sake of simplicity, we omit one important thing right now):
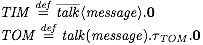
The definitions given above consists of two agents, TIM and TOM. The identifiers of agents are always written in uppercase letters to distinguish them from names, which are always written in lowercase letters. Both agents, TIM and TOM, define a process of how they can communicate. This definition is written behind the equal signs. As can be seen, both agents have the common name talk. Agent TIM has an overlined talk. This denotes that he is a sender on the name talk. A corresponding receiver is written without an overline, like the talk in agent TOM. The communication is always synchronous. This means that agent TIM blocks the execution until some other agent is ready to receive his message and TOM blocks until someone has a message for him. The actual message is represented through another name message. It is written in a different kind of bracket behind the name used for communication. Both agents can communicate and thereby "consume" their names talk. The next step is marked with a dot (.); it divides sequences of actions. The next action for agent TIM is 0. This symbol stands for actually ending the process right now. The agent TIM can't to anything else anymore. Agent TOM has another symbol after he received the message. It is a tau with an subscripted TOM. The symbol tau denotes an unobservable action; it is something that TOM does with the message that we cannot observe. Afterwards TOM also stops execution.
Name Passing
We give the message a bit more meaning and add a third agent that represents a printer. Yes, everything could be an agent, even a printer. The printer agent has its own process like accepting a print job and printing it. To make the situation worse, only agent TIM has access to the printer. The access is represented by the knowledge of the name that is used for communication with the printer agent. The agents are defined as follows (we again omit one important thing):
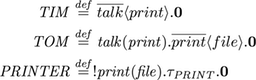
The agent TIM now sends the name print to agent TOM. TOM is now be able to use the received name print as an outgoing communication channel to another agent PRINTER. This is a very important point! There exists no distinction between names for communication and names for the parameters of the communication. As stated, a name could be used for anything! TOM uses the name he received from TIM to send the name file along the name print to an agent named PRINTER. Forget a minute about the exclamation mark at the begin of PRINTER. The agent PRINTER then receives a name file on the name print and processes the file somehow inside of tau subscripted with PRINT. The file is just a name; however it could point to another agent that represents a data-structure. This goes a bit beyond this introduction; right now it is enough to know that the name file somehow represents a file. The agent PRINTER represents a printer. But wouldn't be nice if several agents could send their documents in parallel and the printer queues and prints them one after the other? We do not want to implement a queue in the agent PRINTER; we just would like to state that he can accept several documents in parallel. This is done through the exclamation mark at the begin of the process definition from agent PRINTER. He can accept as many files on the name print as wished. Whenever PRINTER receives a new file it creates a copy of itself. This is called replication.
Choice, Parallelism, and all the Rest
Another important aspect in a process algebra is choice. When we want to specify that agent TIM could talk to TOM - or to another agent called TIL, we could write this as follows:

The summation operator (+) is used to denote the exclusive choice. Either the left or the right part of the operator are chosen for execution. So either the name talk subscribed with TOM or TIL will be used for communication. The agent TIM could model the decision which to chose explicitly with a match operator:
![TIM=[x=true]'talktom<message>.0 + [x=false]'talktil<message>.0](pics/pi-intro4.png)
The match operator [x=y] continues the execution if a name x equals another name y. Agent TIM tests a name x on equality and if this evaluates true he contacts agent TOM. If the expression [x=false] evaluates to true, he contacts agent TIL. It is also possible to send the message from agent TIM to both other agents, TOM and TIL, in parallel:
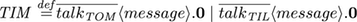
The composition operator (|) executes the left and right part of the operator in parallel. Having introduced this one, we can hint that TIM, TOM, (and the PRINTER) agent need to be placed in parallel to actually interact together (that's it about the important thing left out).
So far we have seen definitions for agents that already contain names; but what if we want to dynamically create names inside an agent? This is done with the special operator v. We define an agent that generates new names on request:
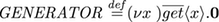
The agent GENERATOR creates a new - and yet unknown - name x, where x is just a placeholder for a new unique name. The agent is able to communicate the new name via the name get. All the way, the generator agent replicates itself, so that it can generate a multiplicity of new names.
What we have considered is only a very basic introduction on how the pi-calculus actually works. There are restrictions on how the operators could be combined as well as much more semantics than explained right now.